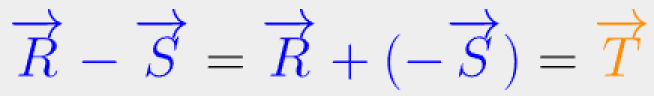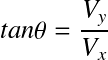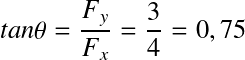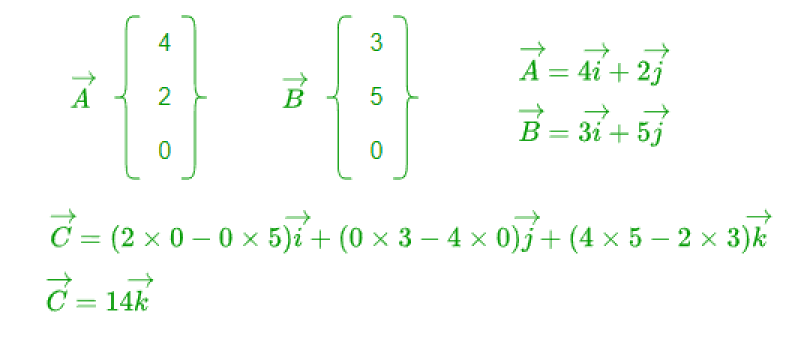Objectifs
Définir les notions de scalaire et de vecteur.
Décrire les principales opérations réalisées sur les vecteurs, les coordonnées cartésiennes d'un vecteur et la notion de vecteur-position.
Définir le produit scalaire et le produit vectoriel de deux vecteurs.
Définition et utilisation
Définition
Définition : Définition
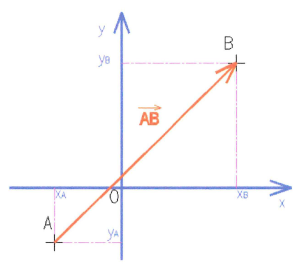
Un vecteur est défini par 4 caractéristiques :
Sa droite d'action,
Son point d'application,
Son sens indiqué par une flèche,
Sa longueur, définie par sa norme ou intensité.
Ce vecteur se note de la manière suivante : ![]() et se dit : « vecteur AB ».
et se dit : « vecteur AB ».
Utilisation
Utilisation en mécanique appliquée
En mécanique, on utilise les vecteurs dans différentes parties :
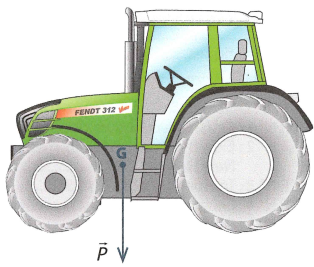
En statique, le vecteur en bleu sur le tracteur désigne l'action de la pesanteur sur le tracteur :
|
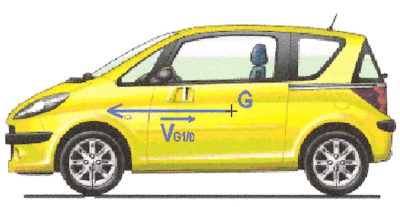
En cinématique, le vecteur bleu désigne la vitesse de la voiture 1 par rapport à la route 0 :
|
Opérations sur les vecteurs
Addition
Définition : Relation de Chasles
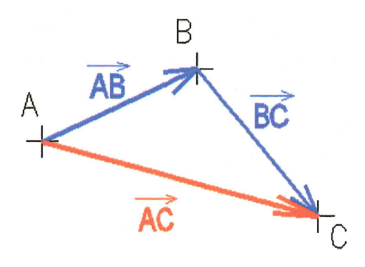
On considère 3 points A, B et C. La relation de Chasles nous permet d'écrire l'égalité vectorielle suivante :
|
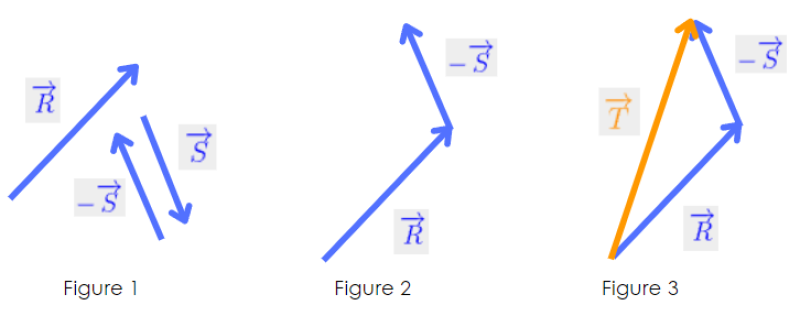
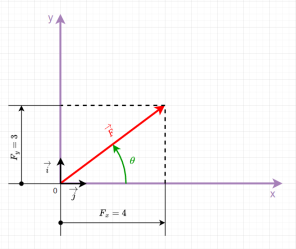
Méthode : Somme de vecteurs
On considère 2 vecteurs ![]() et
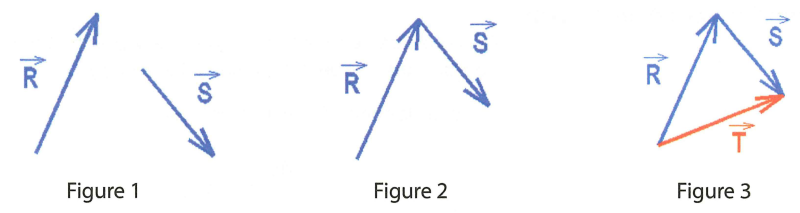
et ![]() que l'on veut additionner. Ces deux vecteurs sont des vecteurs quelconques du plan (Figure 1).
que l'on veut additionner. Ces deux vecteurs sont des vecteurs quelconques du plan (Figure 1).
Pour réaliser la somme de ![]() et de
et de ![]() , il faut les positionner bout à bout (Figure 2). On relie ensuite l'origine du vecteur
, il faut les positionner bout à bout (Figure 2). On relie ensuite l'origine du vecteur ![]() avec l'extrémité du vecteur
avec l'extrémité du vecteur ![]() , on obtient alors le vecteur
, on obtient alors le vecteur ![]() (Figure 3). On a la relation suivante :
(Figure 3). On a la relation suivante :
![]()
Soustraction
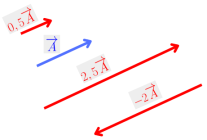
Multiplication d'un vecteur par un scalaire
Définition :
Les sommes ![]() et
et ![]() s'écrivent simplement sous la forme
s'écrivent simplement sous la forme ![]() et
et ![]() , produit des scalaires 2 et 3 par les vecteurs
, produit des scalaires 2 et 3 par les vecteurs ![]() et
et ![]() .
.
De la même façon, on peut écrire ![]() ,
, 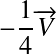 …
…
Exemple :
Si |
Coordonnées cartésiennes d'un vecteur
Repérage dans le plan
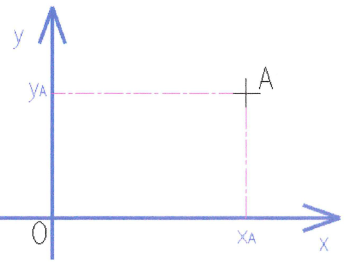
Définition : Coordonnées d'un point
On se place dans le repère (O,x,y). Les coordonnées du point A sont données par les projections de sa position sur les axes x et y : On écrit alors :
|
Définition : Coordonnées d'un vecteur
On considère le repère (O, x, y) et deux points A et B de coordonnées respectives Les coordonnées du vecteur AB s'écrivent :
On dit que l'on utilise les coordonnées de « l'extrémité » moins les coordonnées de « l'origine » du vecteur. |
Définition : Autre façon
Calculs dans le plan
Exemple : Exemple
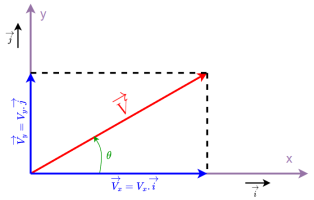
Déterminons le module et la direction du vecteur
Intensité ou norme :
|
Remarque :
![]()
![]()
Produit scalaire de deux vecteurs
Définition
Définition :
Le produit scalaire du vecteur ![]() par le vecteur
par le vecteur ![]() , noté
, noté ![]() , est égal au produit des modules des deux vecteurs multiplié par le cosinus de l'angle
, est égal au produit des modules des deux vecteurs multiplié par le cosinus de l'angle![]() entre leurs directions respectives.
entre leurs directions respectives.
Si :
|
Remarque :
Le produit des deux vecteurs est un nombre ou un scalaire et pas un autre vecteur.
Si ![]() et
et ![]() sont perpendiculaires (
sont perpendiculaires (![]() ), alors
), alors ![]() .
.
Le produit scalaire est commutatif : ![]() .
.
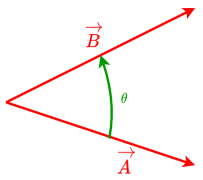
Exemple : Exemple d'un produit scalaire
Produit vectoriel de deux vecteurs
Définition
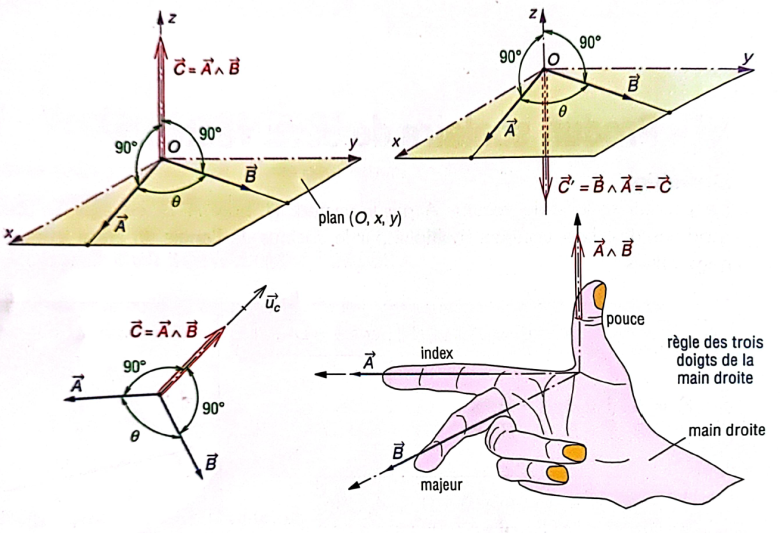
Définition :
Le produit vectoriel du vecteur ![]() par le vecteur
par le vecteur ![]() , noté
, noté ![]() , est un vecteur
, est un vecteur ![]() perpendiculaire au plan
perpendiculaire au plan ![]() et tel que :
et tel que :
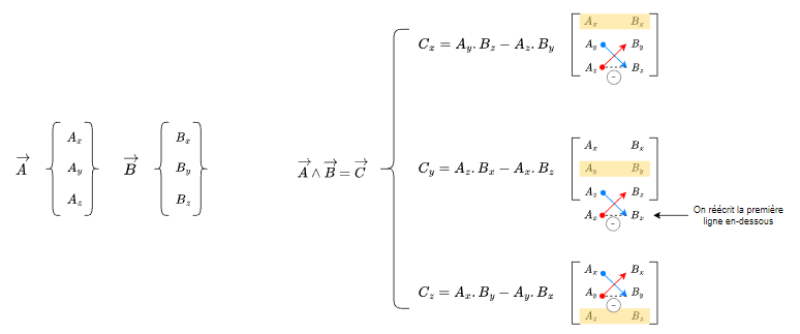
![]() avec
avec ![]()
Remarque :
Si ![]() et
et ![]() sont parallèles, alors
sont parallèles, alors ![]()